Applications
Geothermal benchmarking
Accurate prediction of temperature and pressure distribution is essential for geothermal reservoir exploitation with cold water re-injection. Depending on our knowledge about the heterogeneous structure of the subsurface, the reservoir development scheme can be optimized and the overall lifetime of the geothermal field can be extended. In DARTS, the molar formulation with pressure and enthalpy as primary variables is selected to solve the governing system describing the geothermal model. Besides, the fully-coupled fully-implicit two-point flux approximation (TPFA) on unstructured grids is implemented to solve the mass and energy conservation equations. For the nonlinear solution, we employ the recently developed Operator-Based Linearization (OBL) approach. The solutions of DARTS is compared with the state-of-the-art simulation frameworks using a set of benchmark tests1.
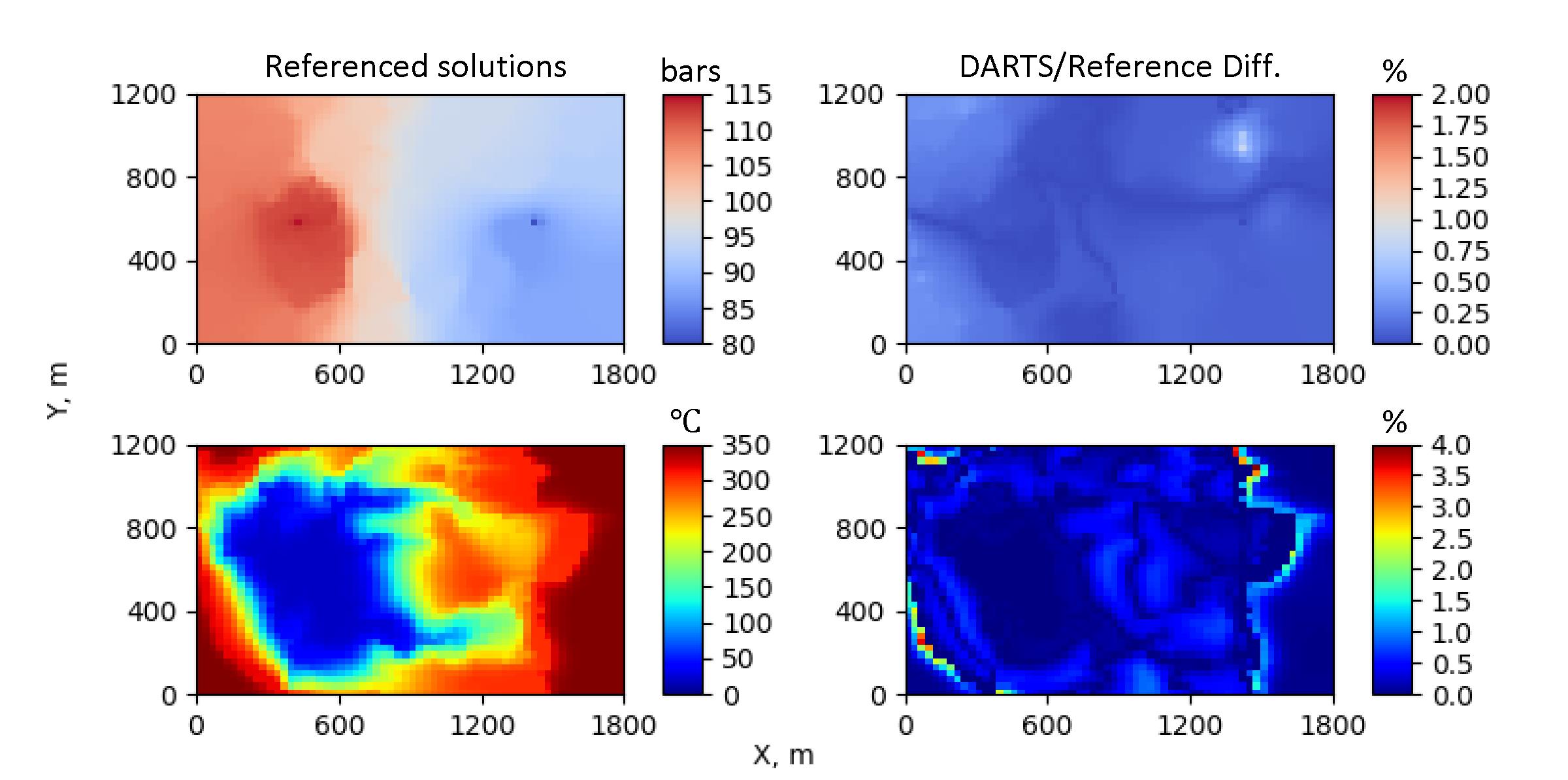
Fig.1: 2D results comparison between DARTS and TOUGH22 for high-enthalpy test case1
DARTS achieves a good match for both low- and high-enthalpy conditions in comparison to TOUGH22, see Fig.1 for example. Similar accuracy DARTS demonstrated in comparison with AD-GPRS3 with an example shown in Fig.2 for elongated in z-direction example of the 3D geothermal reservoir. At the same time, DARTS provides high performance and flexibility of the code due to the OBL approach, which makes it particularly useful for uncertainty quantification in processes involving complex physics.
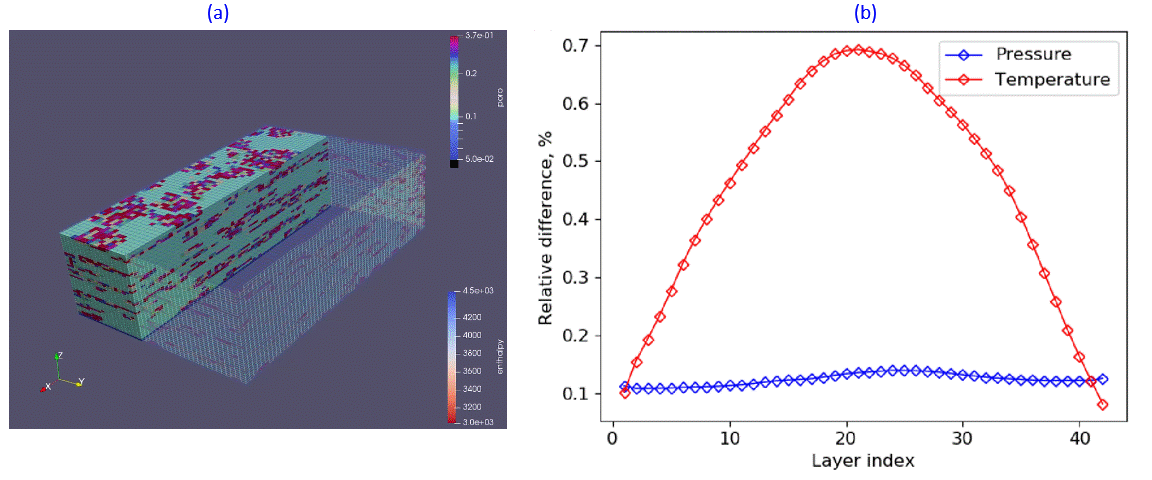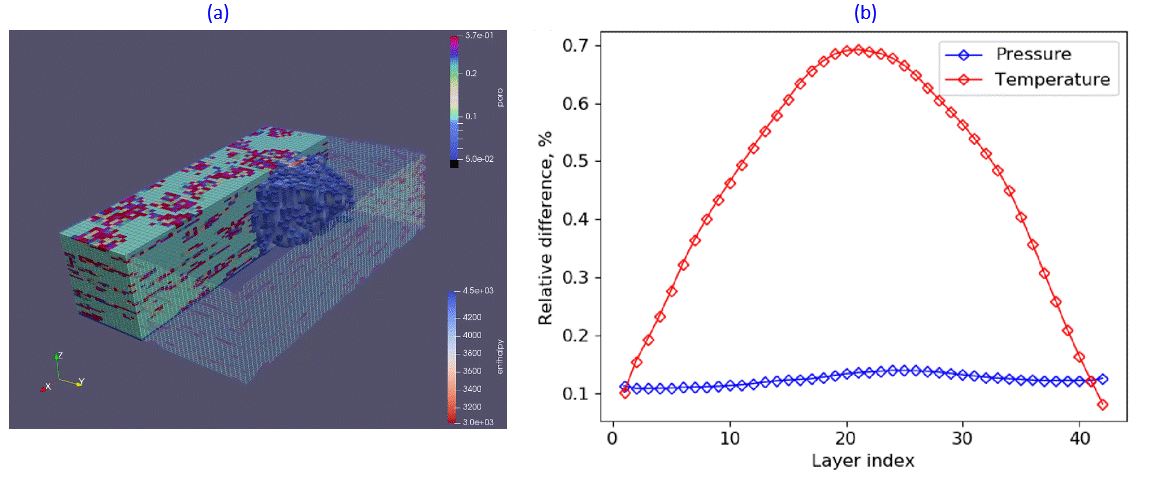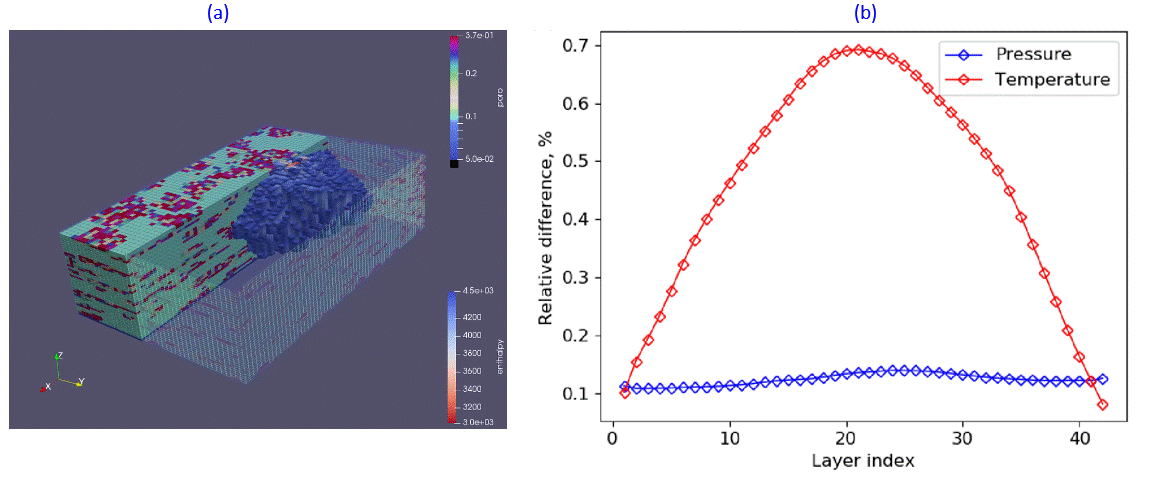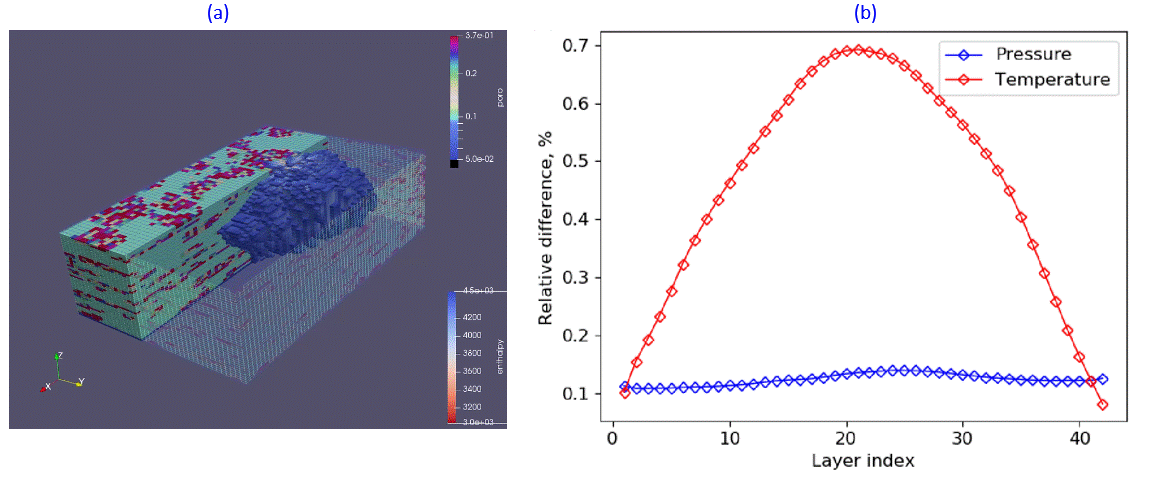
Fig.2: Cold water plum propagation (a) and layer-wise error in comparison with AD-GPRS3 (b).
Sensitivity analysis of geothermal projects
A low-enthalpy geothermal reservoir with complicated realistic sedimentary distribution located in the West Netherlands Basin is utilized to perform sensitivity analysis4. A porosity distribution of the model is displayed in Fig.3. The model mainly consists of Berkel and Delft sandstone (around 0.8 million grid blocks) and shale layers (approximately 2.4 million grid blocks) with several faults. One of the major outcomes from the analysis is the shale layers, which are generally ignored in numerical simulation of hydrocarbon reservoirs, can significantly extend the lifetime (time before thermal breakthrough) of geothermal reservoirs. The results demonstrate the sensitivity of doublet lifetime to these parameters varies from years to decades.

Fig.3: Porosity distribution and thermal front propagation of realistic geothermal reservoir.
The high numerical performance of DARTS makes it possible to run a large ensemble of models at high geological resolution for uncertainty quantification. Besides, the influence of various production regimes (well placement, production rate, etc.) and geological parameters (overburden, permeability-porosity correlation, etc.) to the heat production and doublet lifetime are shown in Fig.4. In overall, spatial heterogeneity of facies in geothermal reservoirs introduces large variability in energy production and demand uncertainty quantification for an accurate prediction of technologic and economic parameters of the process.
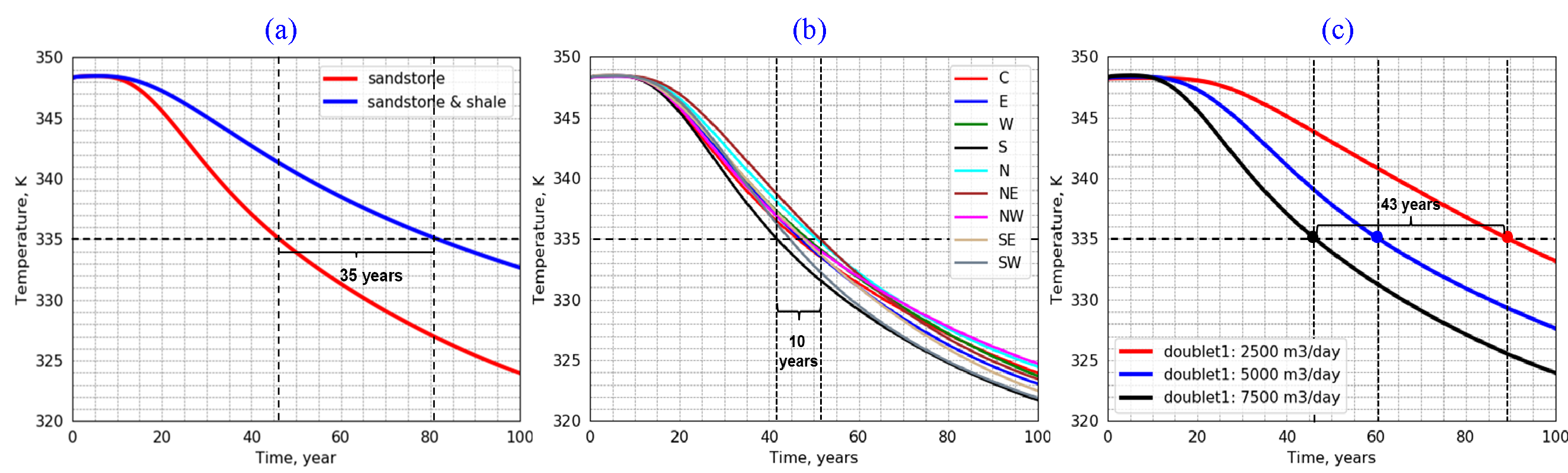
Fig.4: Variation of the double lifetime with three factors: facies (a), well placement (b) and flow rate (c).
Geothermal flow in fractured systems
Multi-phase mass and heat transfers are ubiquitous for modelling of the most energy-related subsurface applications. The presence of complicated fractures may significantly impact, or even determine, the dynamic transport process. Here, the multi-phase flow in a fractured high-enthalpy geothermal reservoir is numerically investigated. The utilized fracture network is sketched and scaled up from digital maps of an outcrop at Whitby Mudstone Formation. The discrete fracture model (DFM) is used to describe the fractured system. Complicate nonlinear physics is adopted to describe the phase transition process (i.e., steam condensation) initiated with cold water injection. The existence of the fracture network magnifies the uncertainty of heat transfer in the reservoir because of a wide range of fracture scales and the complex fracture geometry. To fulfil both accuracy and efficiency in the computation, the resolution of the grid is optimized through results and runtime comparison combined with detailed convergence analysis among different sets of grids. The results of energy depletion in typical carbonate reservoir is shown in Fig.7 for high-enthalpy (super-saturated steam) initial conditions.
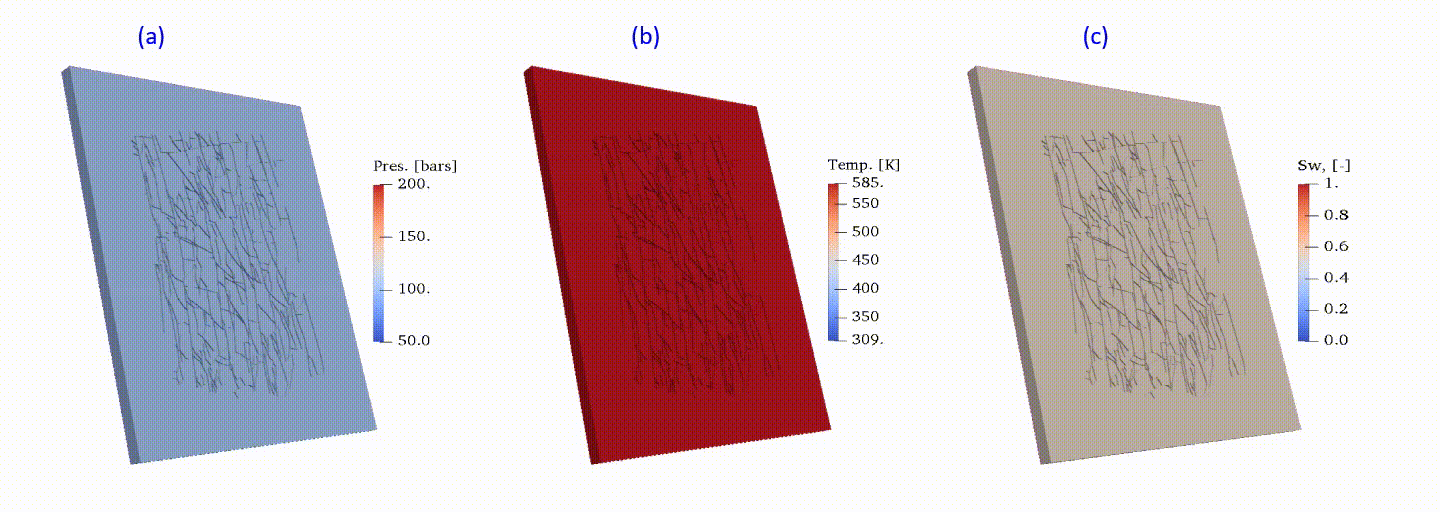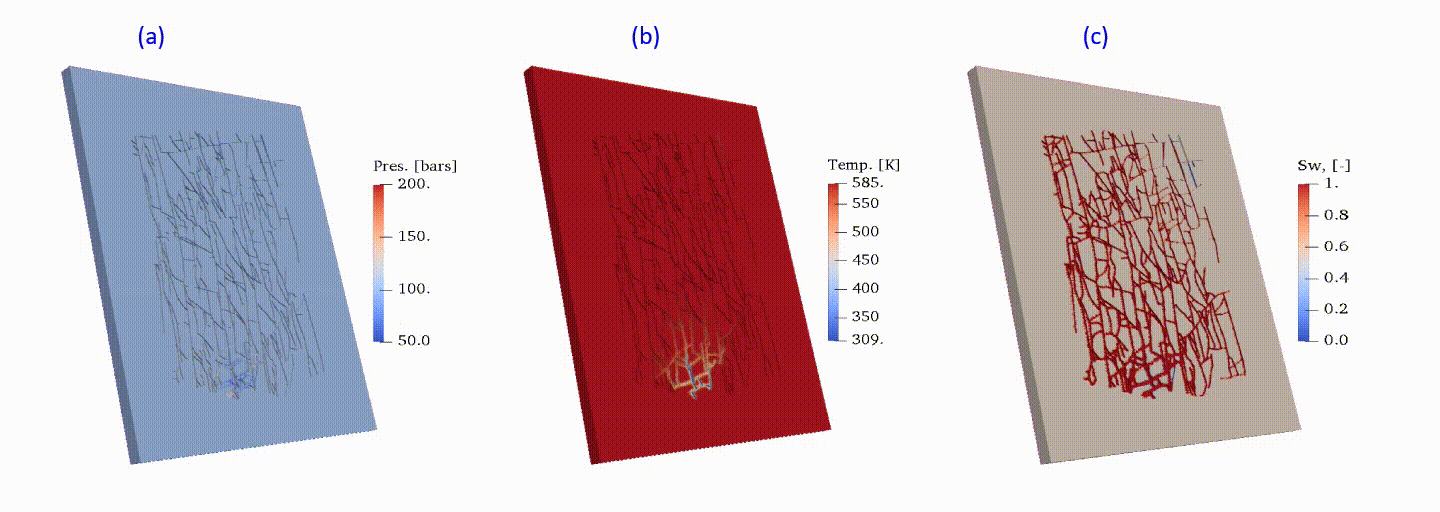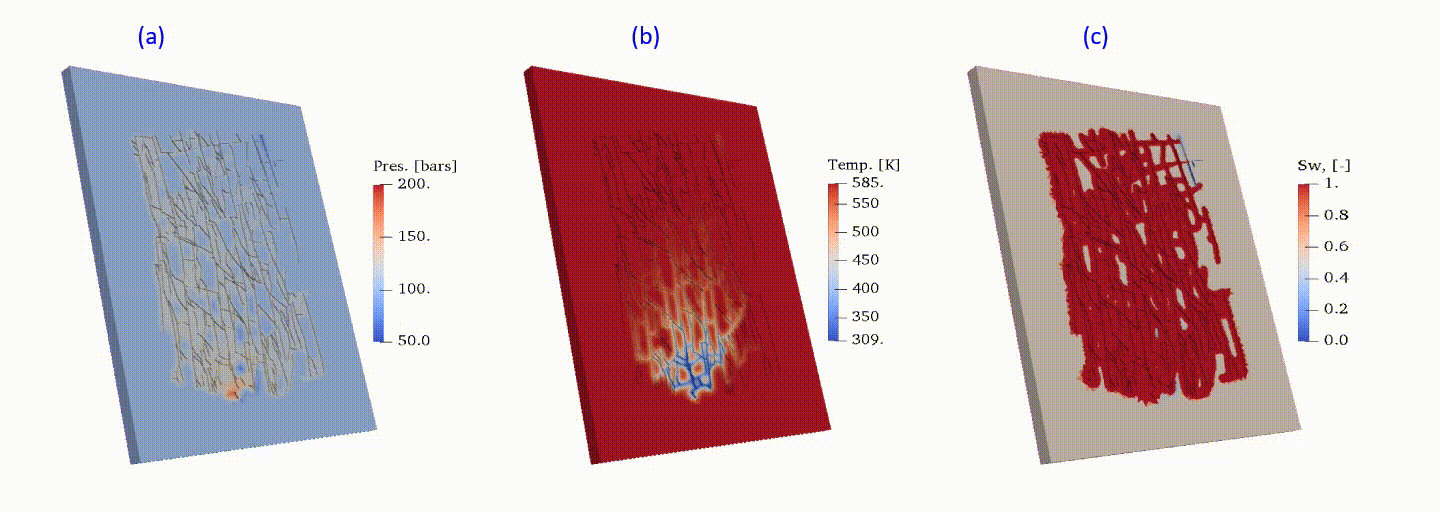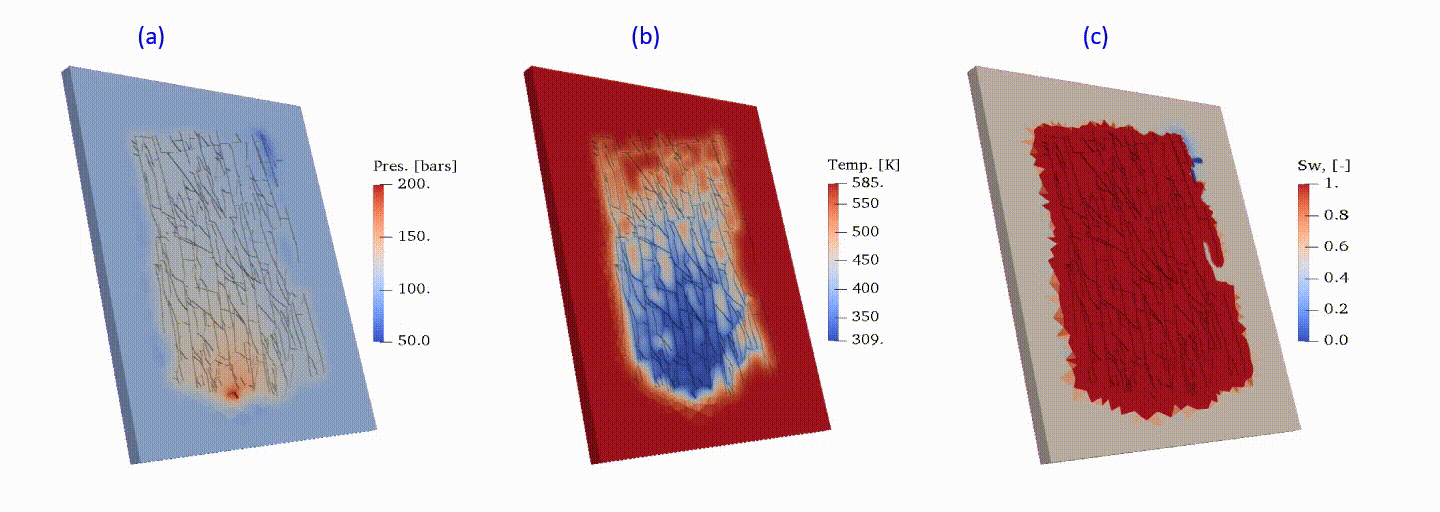
Fig.7: Energy depletion in a carbonate fractured reservoir: pressure (a), temperature (b) and liquid saturation (c).
With the optimal mesh resolution, we investigated the influence of flow rate and thermal parameters on thermal propagation, which are found to be sensitive to the flow rate, rock heat conductivity and heat capacity8 as shown in Fig.8. The findings provide insights for the multi-phase mass and heat transport in the fractured high-enthalpy geothermal reservoirs, which can be taken as guidance for the real geothermal developments with uncertainties.
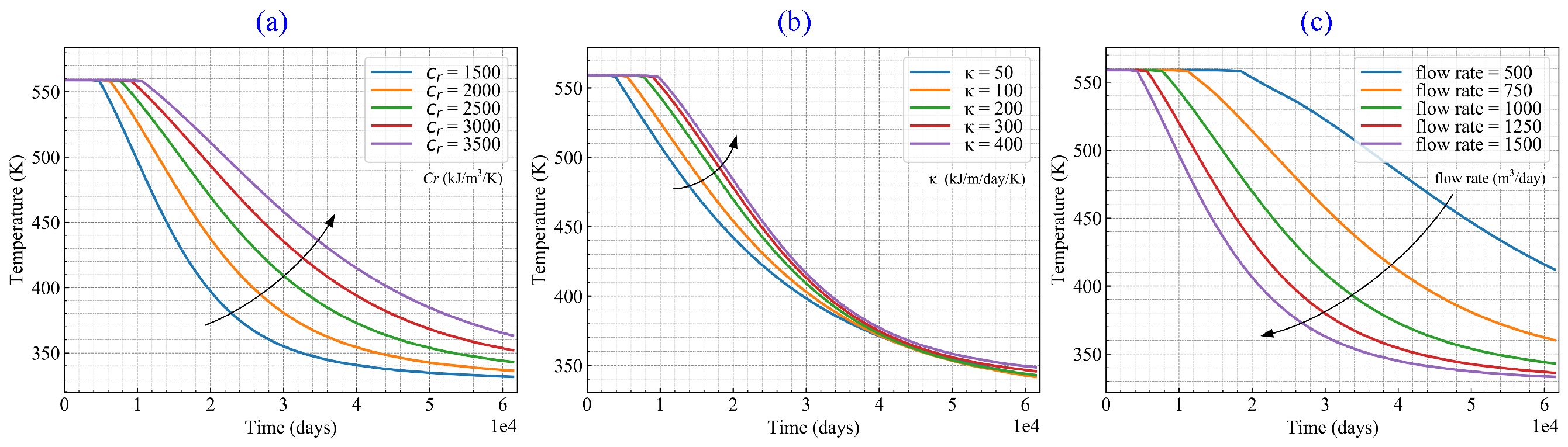
Fig.8: Variation of the double lifetime with three factors: heat capacity (a), heat conductivity (b) and flow rate (c).
Uncertainty quantification for fractured reservoirs
Performing uncertainty quantification on a large (high-fidelity) ensemble of Discrete Fracture Models (DFM) can become computationally unfeasible. With an advanced coarsening strategy for fractured reservoirs, the numerical solution can be evaluated as a different coarse level with a certain gain in simulation performance. In terms of main flow patterns, it is therefore expected that the resulting coarser representations are still very much suitable as a diagnostic tool for classifying the full ensemble of models. In Fig.9, the temperature distribution for geothermal application in typical carbonate reservoir is shown for four ensemble members at coarse and fine scales.

Fig.9: Temperature distribution for four members of ensemble at fine (upper row) and corse (lower row) scales.
Using the well rates, pressure, and field-scale production data from the coarse simulation results, a clustering algorithm can be performed to select ensemble representatives based on continuous Multi-Dimensional Scaling9. Once the ensemble representatives are determined at a certain coarse scale (relative fast procedure), the full stochastic response can be reconstructed for fine-scale. In Fig.10, this procedure is illustrated for full ensemble with members shown in Fig.9.
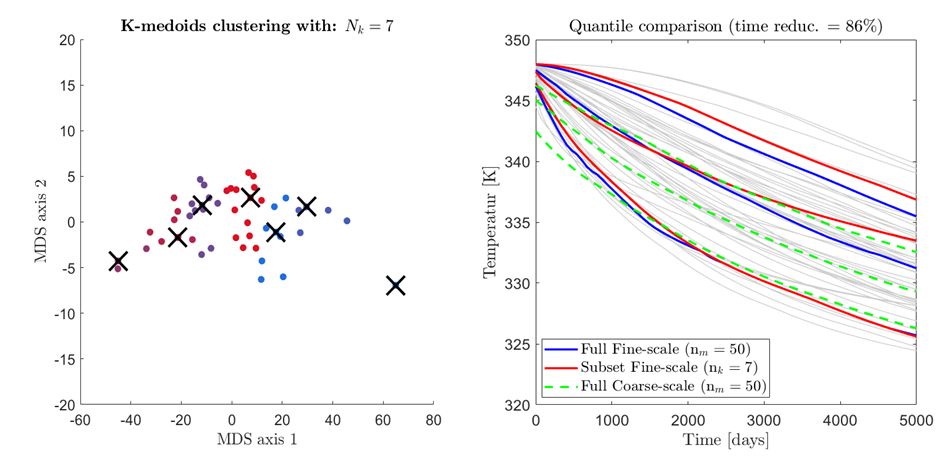
Fig.10: Clustering of MDS distances for coarse (a) and reconstruction of stochastic response at fine scales (b).
Supercritical CO2-brine interactions
Geological storage of CO2 is a crucial and upcoming technology to reduce anthropogenic greenhouse gas emissions. Due to the buoyant characteristic of injected gas and the complex geology of subsurface reservoirs, the security of underground storage is a major concern. To assess the security of CO2 storage, an accurate prediction of the CO2 plume migration is essential. In this study, an accurate thermodynamic model is developed to describe realistic gas behaviour in a saline aquifer and to understand the factors affecting CO2 storage. A recently developed thermodynamic model is based on a combination of Peng-Robinson10 and Kritchevsky-Illiinskaya11 equations of state. This model combines classic fugacity-based formulation for the supercritical gas phase and activity model combined with Henry's constants for the aqueous brine.

Fig.11: Supercritical CO2 dissolution in realistic 3D model of aqueous aquifer.
The phase behaviour based on this thermodynamic model and a consistent set of physical properties has been implemented in DARTS. An example of an enhanced dissolution of supercritical CO2 in a geologic aquifer is illustrated by an unstructured 3D model shown in Fig.11. The model can accurately capture a phase behaviour in supercritical CO2-brine-impurity system and predict an enhanced dissolution rate for the variety of changing parameters including pressure, temperature and salinity of brine. The enhanced dissolution rate in realistic 3D conditions is different from its 2D analogue. This model can be fully coupled with chemical reaction relevant to CO2 sequestration12 for longer time-scale predictions.
Multiphase flow and reactive transport
We introduce an efficient element based reduction technique for molar formulation. The chemical equilibrium constraints are included into the multiphase multi-component flash calculation which solves the thermodynamic and chemical phase equilibrium simultaneously13. This provides a generic treatment of chemical and thermodynamic equilibrium within the successive substitution loop of multiphase flash to accommodate chemical precipitation and dissolution. Using the Equilibrium Rate Annihilation matrix allows us to reduce the governing unknowns to the element conservation equations while the coupling between chemical and thermodynamic equilibrium is captured by modified multiphase flash equations.
A finite-volume unstructured discretization in space is applied together with a fully-implicit approximation in time. The resulting complex nonlinear system is parameterized using the OBL approach. In OBL, the time-consuming phase and chemical equilibrium computations are significantly decreased which reduce linearization time and the number of nonlinear iterations. Besides, equilibrium reactions are fully coupled with kinetic reactions in DARTS. Fig.12 presents several examples where equilibrium reactions describing the dissolution in carbonates are compared with the kinetic reactions at different kinetic rates.

Fig.12: Dissolution with equilibrium (a), high-rate (Da~10) kinetic (b) and lower rate (Da~0.001) kinetic reactions.
Another example in Fig.13 presents kinetic dissolution in the complex fractured system at different aperture distribution decreasing from (a) to (c). In Fig.13,a, the acidic fluid is propagated by fracture system to the right border while in Fig.13,c, fractured system is almost closed and plays the role of permeability perturbation.
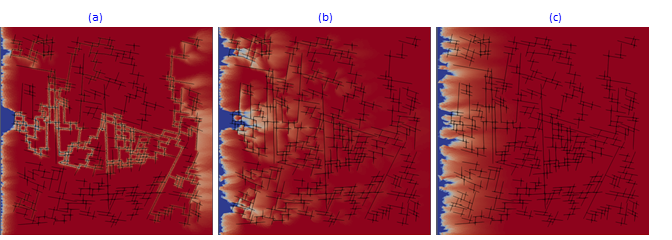
Fig.13: Kinetic dissolution in fractured reservoir with fractures apperture changing from 1 mm (a) to 0.5 mm (b) and finally to a fully closed system (c).
Modeling of dissolution in core
Acidizing is a widely used technique for intensification of wells. At certain conditions, acid injection results in a formation of highly conductive channels, e.g. wormholes. The associated rock matrix dissolution is highly nonlinear and may influence the fluid flow as well as rock properties. Wormhole patterns and breakthrough time are mainly controlled by acid strength and injection rate. We developed a fully implicit method (FIM) to numerically solve the reactive flow and transport problem coupled with equilibrium and kinetic reactions associated with the acid injection. The developed framework is aimed to predict a pattern of dissolution as well as wormhole breakthrough time. For an accurate description of species interactions, we directly connect PHREEQC equilibrium computation with FIM framework for kinetic dissolution using an element balance approach13. This coupling was achieved with an application of an Operator-Based Linearization scheme14 utilized within DARTS.
The developed solution is validated against experimental study14, which also includes the full physics numerical model. Results are given in Fig.14. Two numerical results obtained starting from the same porosity distribution but processed by very different technique demonstrate similar wormhole formation.
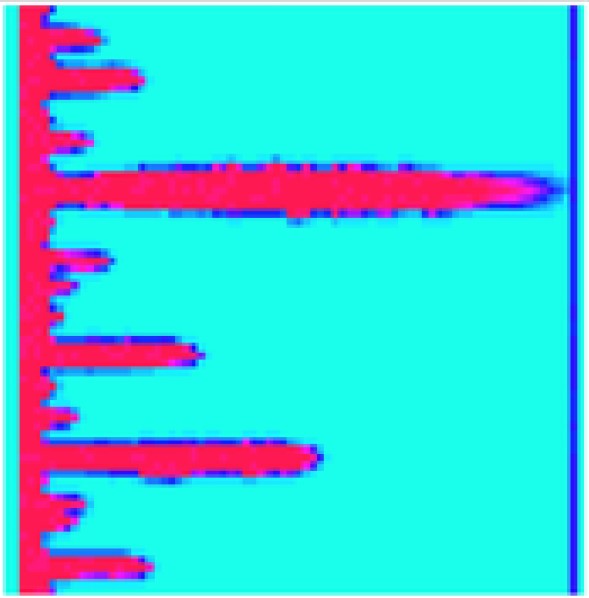
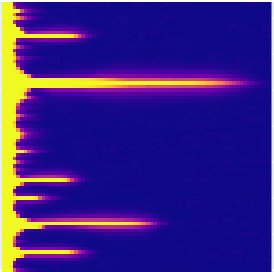
Fig.14: Simulation of wormholes starting from the same initial porosity distribution with (a) sequential coupling15 and (b) fully implicit method (DARTS).
Full 3D model for dissolution in the core is shown in Fig.15. Main criteria for validation are wormhole breakthrough time and amount of rock matrix dissolved. A qualitative comparison shows a reasonable match in terms of break-through time and competing wormholes spatial distribution. The wormhole formation and propagation are accurately captured in high-resolution 3D geometry.
Fig.15: 3D simulation of wormholes (a) and results of experiments (b).
Modeling of foam experiments
Foam improves significantly the sweep efficiency of gas injection. Foam-oil displacement in reservoirs involves strongly nonlinear physics, e.g. multiphase flow and transport with oil-foam interactions. The nonlinearity of this process challenges conventional simulation, which often translates into a high computational cost. To address this problem, we extend an Operator-Based Linearization (OBL) approach for simulation of foam EOR processes. Foam in porous media is described using an implicit-texture model with two flow regimes. The OBL approach is applied to reduce the nonlinearity of the foam problem. We validate the numerical-simulation results using three-phase fractional-flow theory for foam-oil flow. We conduct a series of numerical validation studies to investigate the accuracy and efficiency of the proposed approach. The OBL foam model shows good agreement with analytical solutions at different conditions and foam parameters as shown in Fig.16.
Fig.16: Comparison between analytical solution and simulation results. The upper figures are composition path (fmoil=0.3) in ternary diagram, and the lower row are saturation profile at given PVI.
The validated foam model was used for predictive modelling of foam core experiments. The porosity of core was reconstructed based on the difference between wet and dry scans16. Next, simulation of oil displacement by foam was modelled and compared with experimental results17. As shown in Fig.17, foam creates oil banks which prevent gas from escaping. In overall, both simulation and experimental results have a reasonably good match.

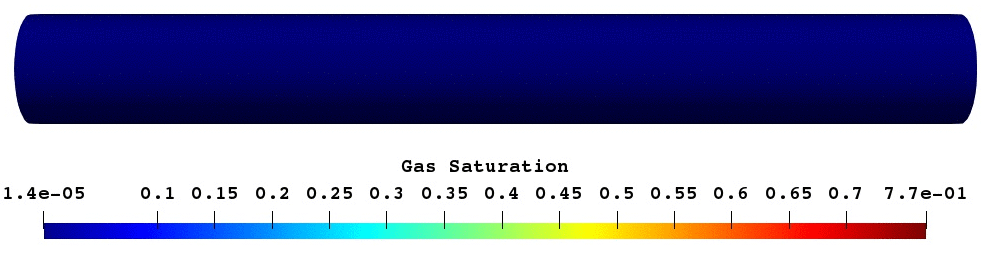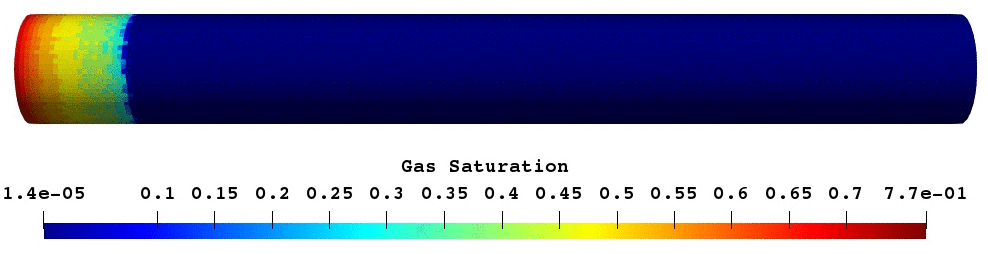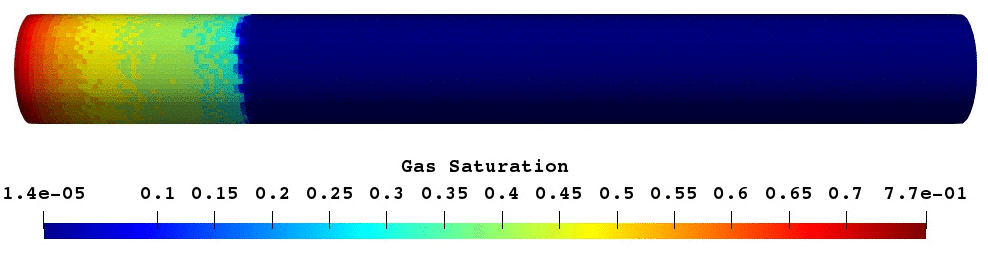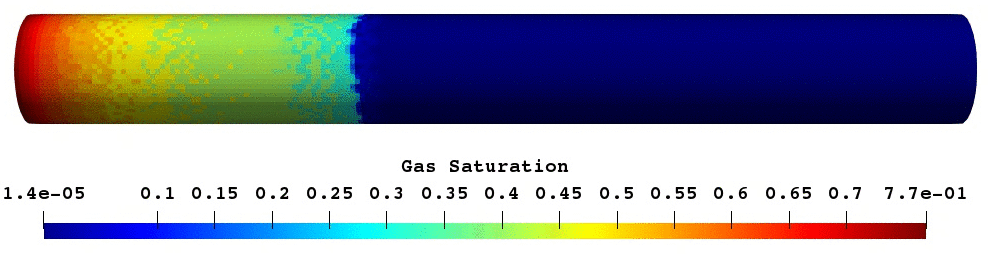

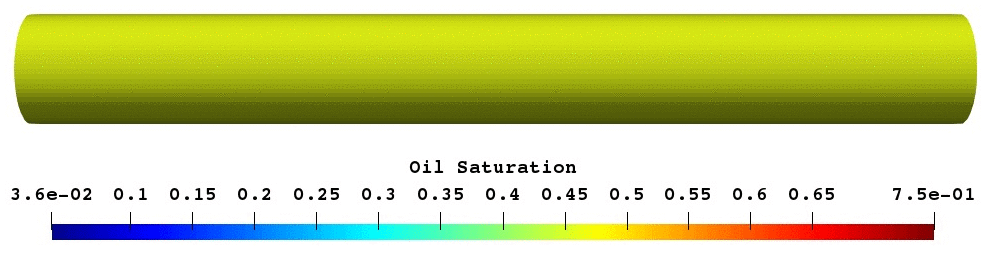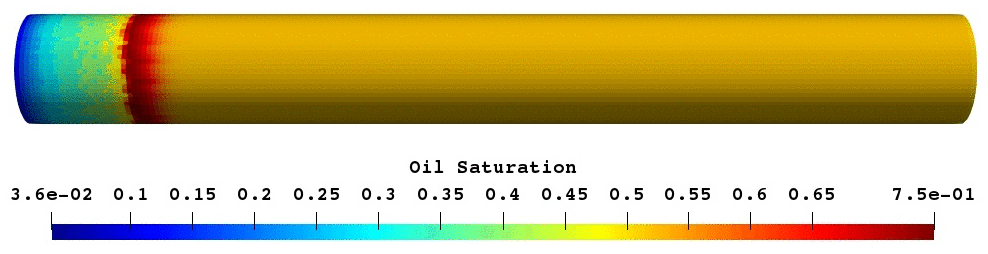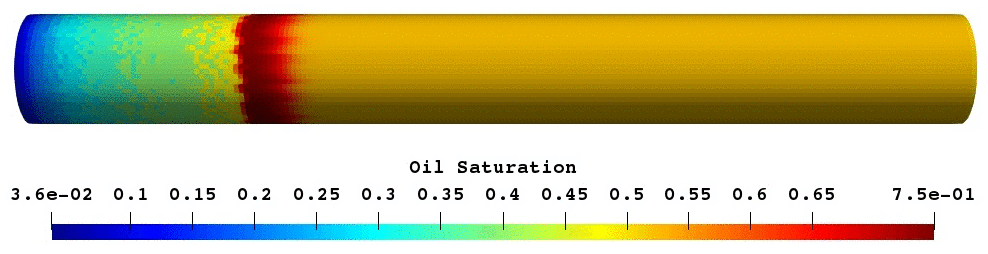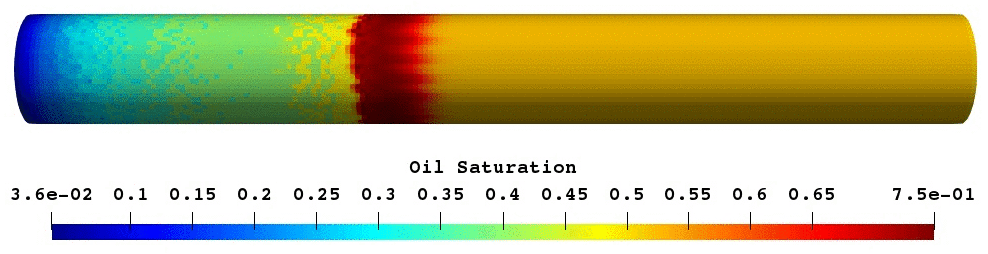
Fig.17: Gas saturation and oil saturation profile at the given PVI.
Physics-based data-driven models
We propose a novel approach where a proxy model combines limited information about a spatial configuration of the hydrocarbon field and a simplified description of the governing physics. The approach contains several stages: in the first, the spatial connectivity graph is generated based on positions of wells and a limited log interpretation. Next, unstructured gridding is applied for the construction of spatial connectivity graph. The governing physical description is integrated using Operator-Based Linearization (OBL) approach. The parameters of this proxy model are regressed to the observation data using gradient optimization assisted by machine learning.
The proposed approach is validated based on high-resolution Brugge-field model18. The synthetic production data for the training period was generated based on high-fidelity model run with varying BHP controls following the original Brugge model schedule with a 5% white noise imposed to resulting oil and water rates. The discretized model for high-fidelity Brugge-field and proxy model is shown in Fig.18. Here, the number of control volumes decreased by more than two orders of magnitude.
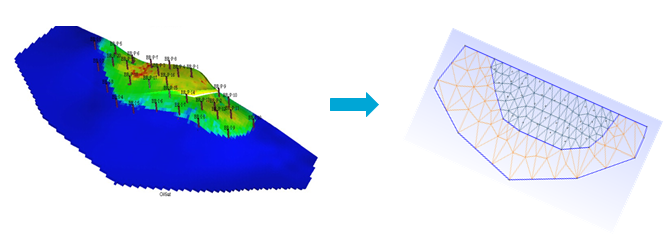
Fig.18: High fidelity Brugge model, used to generate truth model response (139x48x9 grid blocks) (a) and unstructured proxy model with 283 elements only (b).
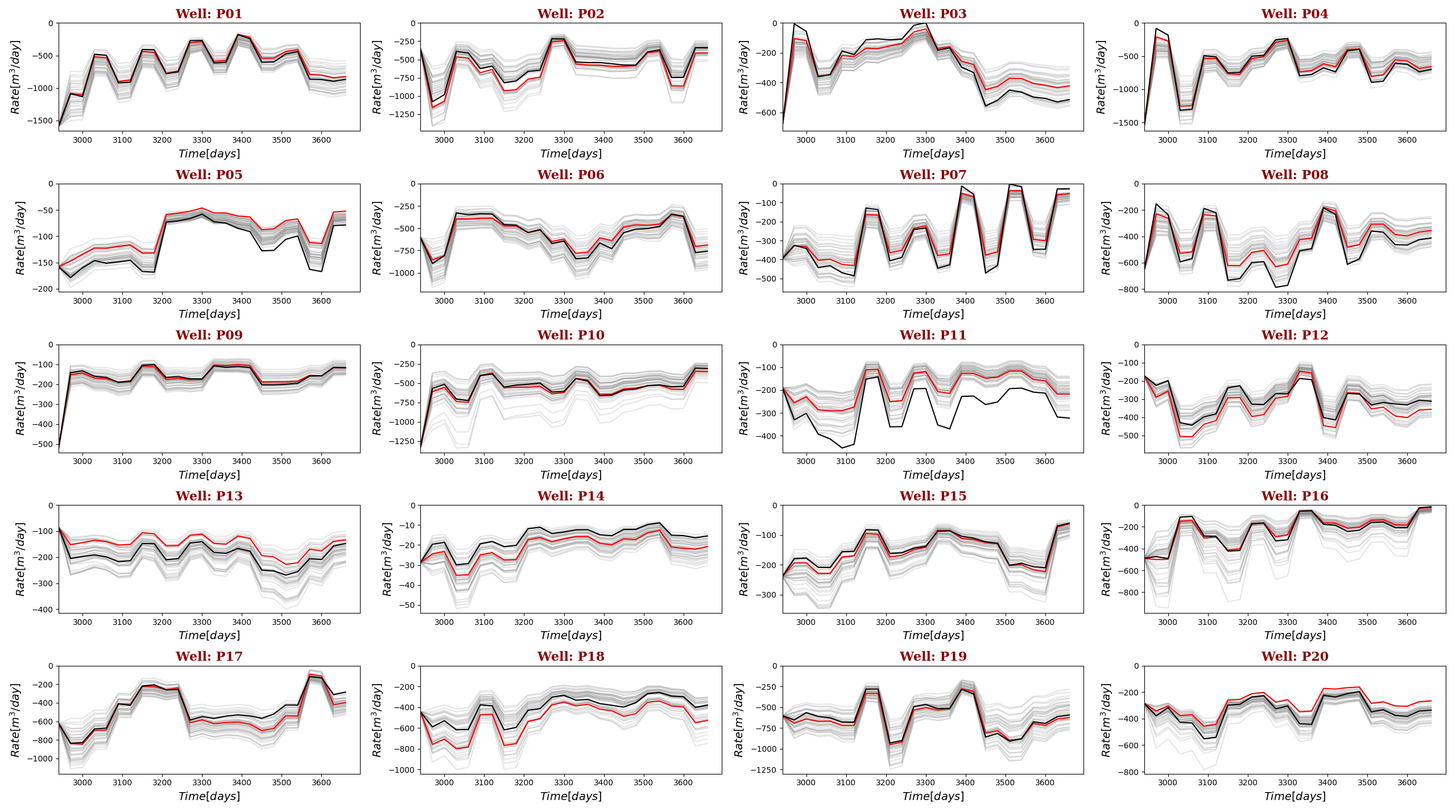
The resulting proxy model performs three orders of magnitude faster when applied in production optimization in comparison to the high-fidelity model (0.03 vs. 97.3 sec). Fig.19 illustrates a two-year production forecast for high-fidelity and trained proxy model which indicate relatively accurate rate prediction for all 20 production wells. Notice that in the case of data-driven models, underlying geological information was never used.
 DARTS - Delft Advanced Research Terra Simulator
DARTS - Delft Advanced Research Terra Simulator