Capabilities
Check the recent presentation video where an observation of the technology behind DARTS is given. Several projects perfromed with DARTS and relevant to Energy Transition are discussed as well.
Structure of simulation framework
The key element of DARTS is operator-based linearization (OBL)1. The state-based terms of governing equations are parametrized in the physical space of the problem forming dynamically expanding lookup tables where the supporting points for reconstruction of operators are saved in a special two-level sparse storage designed for efficient lookup and re-use. These tables are used in linearization to approximate operators along with derivatives with respect to governing unknowns using piecewise multilinear interpolation in physical space. It allows to detach fluid and rock properties calculations (now only performed at supporting points) from the main nonlinear loop and to relax the performance requirements for such calculations.
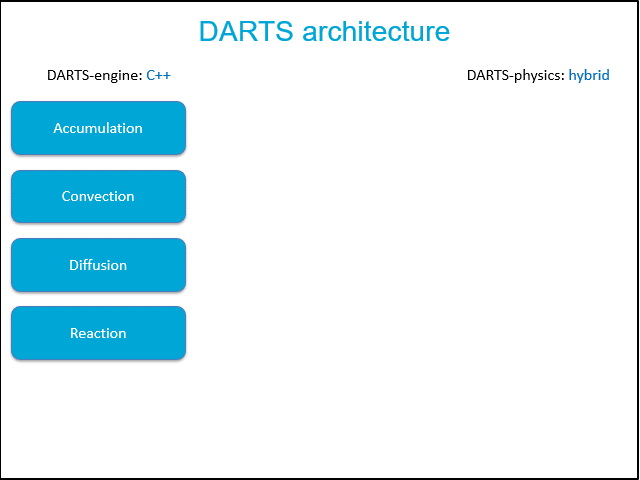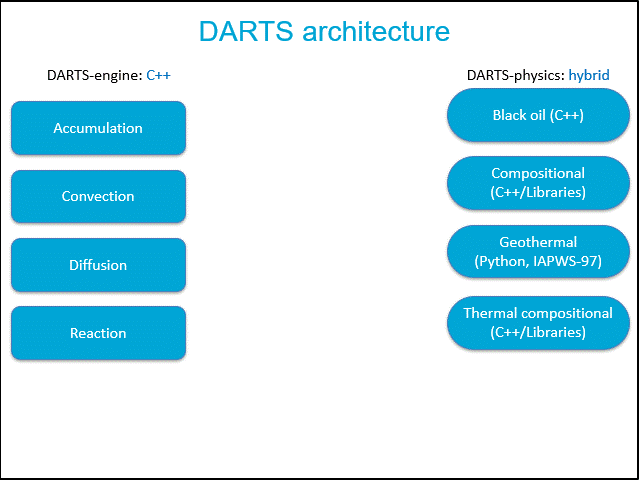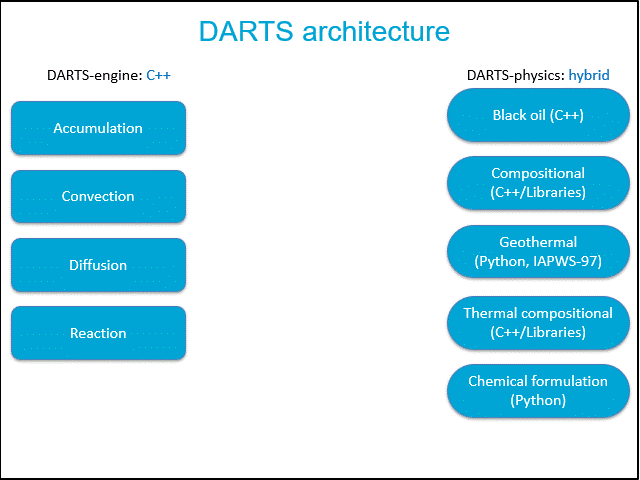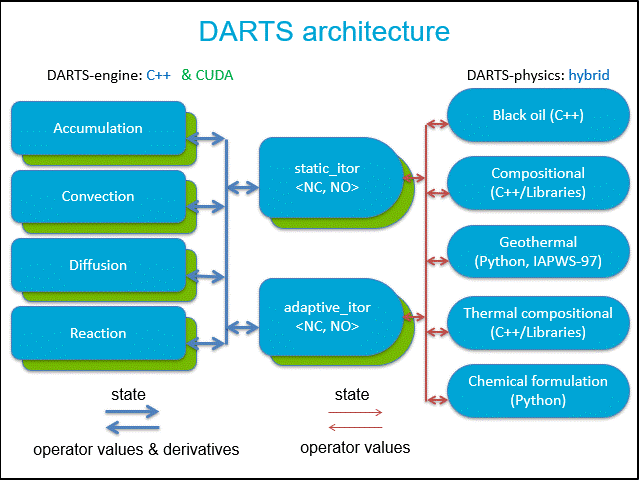
Fig.1: Structure of two main DARTS packages: DARTS-engines and DARTS-physics.
The modular structure of DARTS is demonstrated in Fig.1. On the left, four main components (available physical terms) defining simulation engine are shown. On the right, main five models involved in physical package are listed. Depending on the simulation type, different combination of physical terms in governing partial differential equations and corresponding operators supported by physical package may be required. For example, in geothermal applications, accumulation, convective flux and diffusive (conductive) temperature are required for conservation equations for mass and energy.
Two types of interpolators connect engine and physics. Static iterator pre-computes all supporting points in advance being useful for coarse physical representation and low-dimensional parameter space. Adaptive iterator computes only actually required supporting points along the simulation2. When an engine requires values and derivatives of operators for Jacobian and RHS assembly, the interpolator computes them based on the multi-linear interpolation among existing supporting points. Only when some of the required supporting points are missing, the interpolator requests them from physics module. In this case, operator values computed during simulation can be stored and loaded, which can be extremely beneficial in case of running multiple models with the same physical properties (e.g. in optimization process).
Implementations on GPU
Various novel computing architectures, like massively parallel and multi-core, as well as computing accelerators, like GPUs or TPUs, continue to emerge regularly. In order to harvest the performance benefits of these architectures to the full extent and speed up the simulation, the source code has to be inevitably rewritten, sometimes almost completely. The biggest challenge here in terms of complexity, variety and size is linearization procedure since it depends on the governing equations, choice of primary unknowns, physical/chemical phenomena taken into account, and other factors. Here we present a version of DARTS fully offloaded to GPU device with efficient linear and nonlinear solvers.
Previously implemented linearization procedure at GPU device3 was recently complimented with advanced linear solver. At the moment, DARTS is capable of performing the solution of the linear systems arising from any existing physical engine entirely on GPU. Using publicly available cuBLAS, cuSPARSE and AMGX libraries, complemented by our own developed two-stage CPR reduction preconditioner, the linear solver is capable to run 10x-15x faster than on a CPU for large enough models. Fig.2 shows the perfromance of simulation on full SPE10 model with the original dead-oil physics (~2.2M unknowns) and compositional physics representing supercritical CO2 injection for Enchanced Oil Recovery (~4.4M unknowns).
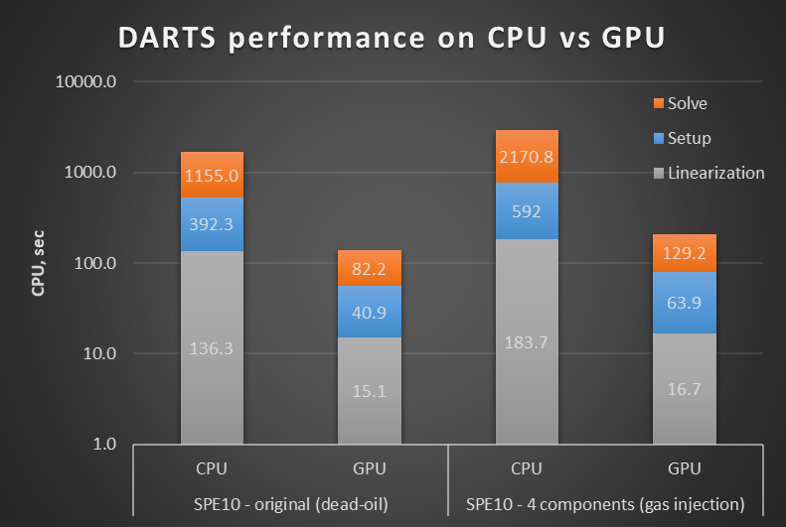
Fig.2: DARTS simulations on CPU and GPU (in log scale) for the SPE10 reservoir with original dead-oil (2 equations per block) and compositional (4 equations per block) physical kernels.
These results were obstained on Intel(R) Core(TM) i7-8086K (4.2 GHz) processor with NVidia GeForce RTX 2080 Ti card. Notice that this performance achieved with a gaming-class GPU card (~€1000 worth) which is pluggable to a regular desktop. Using such a card, the total time required for the solution of the full SPE10 comparative problem becomes less than 3 minutes. With this extension, DARTS provides the flexible, modular, computationally efficient modeling package for various applications, including hydrocarbon2 and geothermal4 energy production.
Adaptive Mesh Refinement
A coupled description of flow and thermal-reactive transport is spanning a wide range of scales in space and time, which often introduces a significant complexity for the modelling of such processes. Subsurface reservoir heterogeneity with complex multi-scale features increases the modelling complexity even further. Traditional Algebraic Multiscale techniques are usually focused on the accuracy of the pressure solution and often ignore the transport. Improving the transport solution can however be quite significant for the performance of the simulation, especially in complex applications related to thermal-compositional flow. The use of an Adaptive Mesh Refinement (AMR) enables the grid to adapt dynamically during the simulation, which facilitates the efficient use of computational resources. This is especially important in applications with reactive flow and transport where the region requires high-resolution calculations as often localized in space.
In this work, the aim is to develop an AMR framework for fully-implict general-purpose reservoir simulation. The approach uses a multi-level connection list and can be applied to fully unstructured grids5. The adaptivity of the grid in the developed framework is based on a hierarchical approach. First, the fine-scale model is constructed, which accurately approximates all reservoir heterogeneity. Next, a global flow-based upscaling is applied, where an unstructured partitioning of the original grid is created. An example of two hierarchy levels for unstructured grid is shown in Fig.3. Once the full hierarchy of levels is constructed, the simulation is started at the coarsest grid. Grid space refinement criteria can be developed specifically for a particular application of interest. The multi-level connectivity lists are redefined at each timestep and used as an input for the next.

Fig.3: Two-level hierarchy for AMR on unstructured grid and corresponding solution at fine, AMR and coarse scales with dynamic adaptivity of levels.
The developed Adaptive Mesh Refinement framework was implemented in DARTS6. The performance of the proposed approach is illustrated for geothermal applications shown in Fig.3. Here adaptive coarsening can accurately reproduce the fine scale solution using 40% less degrees of freedom which expected to bring a proportional improvement in simulation time due to the reduction in the size of the linear system.
Multi-segment wells
Accurate well and near well modelling becomes essential in the reservoir simulation. Recently, advanced (smart) well operations and technologies are employed in the subsurface industry such as long deviated, horizontal and multi-lateral wells. In order to use such technologies intelligently, there must be a robust, supportable model that capture efficiently physics and the expected production scenario. We design a numerical framework for predictive simulation and monitoring of hydrocarbon and geothermal wells based on the general Multi-Segment well (MS-well) model7 which is able to describe the well topology and accurately represent the thermal multiphase multicomponent flow and transport behavior in the wellbore.
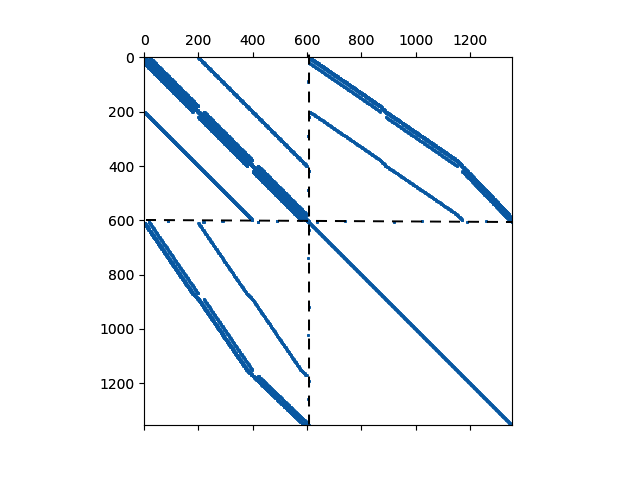
Fig.4: Jacobian matrix for a small 3D structured reservoir and Multi-Segmented well with blocks corresponding to conservation and momentum equations in reservoir and well segments.
Our simulation model is based on the the general unstructured grid framework following the general decoupled velocity formulation. We segment any wells into nodes and connections similar to finite-volume discretization of reservoir flow. Total velocity serves as additional nonlinear unknown and constrained with the momentum equation. The resulting Jacobian structure contains two parts corresponding to conservation and momentum equations as shown in Fig.4. Decoupled velocity formulation based on general unstructured mesh allows us to model complex geometry and take into account arbitrary flow direction, whereby the flow direction is determined dynamically during the nonlinear iterations. Moreover, transforming both reservoir and well nonlinear governing equations into operator form benefits from OBL techniques and reduce further the computational cost related to linearization. Our MS-well model is fully coupled with various physics incorporated in DARTS including chemical reactions with precipitation and dissolution of solid (mineral) phases.
Advanced processing of fractured networks
Current Discrete Fracture Model (DFM) implementation in DARTS relies on a Two-Point Flux Approximation (TPFA) scheme where fractures are represented explicitly in the numerical model 5. However, explicit representation of the fractures contains complex fracture intersection which in turn might pose meshing difficulties. The resulting mesh, therefore, can contain abundant artefacts which negatively impact the performance of the reservoir simulator. Performance issues mainly manifest as numerical inaccuracies due to non-orthogonality of the control-volume intersections. Secondly, it also manifests in terms of convergence problems due to the extremely large contrast between control volumes sizes as shown in Fig.5 for the realistic outcrop data. All these problems are solved by using a pre-processing method6 in which we sequentially process each fracture, using the desired meshing accuracy (predefined size of the fracture segment).
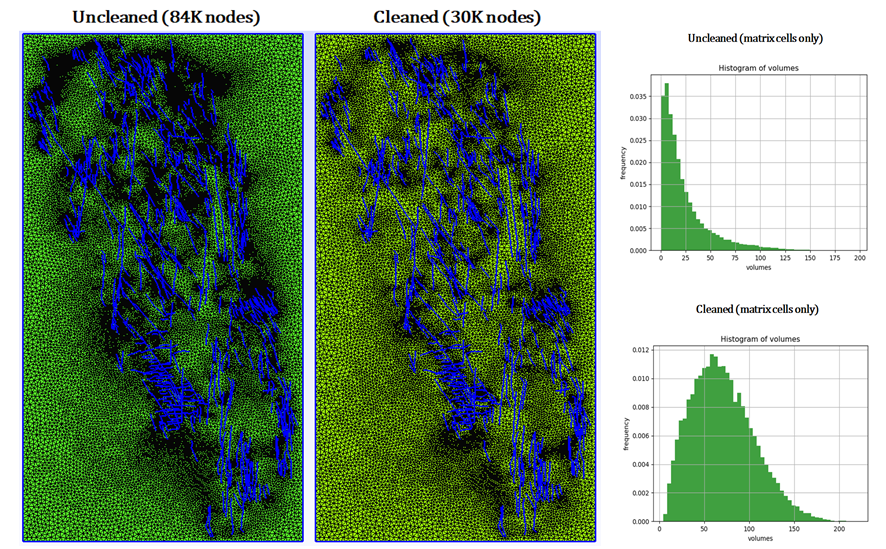
Fig.5: Original version of Brejoes outcrop characterization (a) and processed version (b) with corresponding statistics of control volume sizes for both of them (c).
The sequential algorithm adds each fracture line split on segments and resolves all conflicts when segments are close to each other by merging them. The computational time of the pre-processing step is insignificant to simulation time while still greatly improving the simulation results (both accuracy and performance). The result of such pre-processing is shown in Fig.5,b. With this approach, it is possible to construct a discrete fracture network at any desired resolution while maintaining the main characteristics of the original fracture characterization. As can be observed in the Fig.6 for a realistic outcrop data7, minimal information on the fracture network is lost in the processing at a coarser level while the number of degrees of freedom in the model is reduced by several orders of magnitude.

Fig.6: Processing of realistic outcrop at different meshing resolution with corresponding degrees of freedom.
Adjoint gradients with OBL
This study focuses on adjoint-based gradient optimization9 using operator-based linearization (OBL) method. The objective function is augmented by being linearly combined with reservoir state equations. This objective function shares the same extrema with the original objective function as the residual of reservoir state equation is equal to zero. In the course of calculating the gradient of objective function, several derivatives with respect to state variables and control variables at each time step are provided by OBL technique. OBL method largely reduces the amount of property-related computations by interpolating the state-based terms of governing equations and their derivatives with respect to governing unknowns in physical space.
As an example, a history matching problem of gas injection problem10 using adjoint gradient with OBL is investigated. The proposed method helps to efficiently calculated the gradient of objective function, especially for the case with large amounts of elements in control variables and for many components. For a visualization purposes, we investigate 1D reservoir with only two permebaility values u1 and u2 in the vector of control variables. The surface plots of objective function values are shown in the Fig.7.
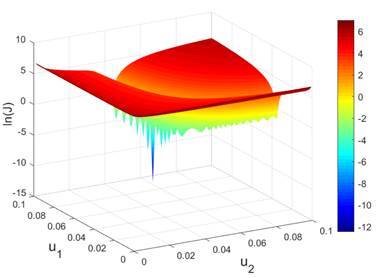
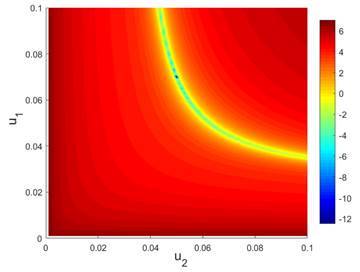
Fig.7: The plots of objective function values in 3D (left) and 2D projection (right).
As it can be seen in the above figures, there is a clear band area which corresonds to the global minumum the objective function. Besides, there is also a bunch of local extrenums near the global minimum. In the Fig.8 we show the solution trajectories based on numerical and adjoint gradients. Both methods behave almost identical and require most of the computational efforts in this band area with many local extrenums before finding the global optimum.
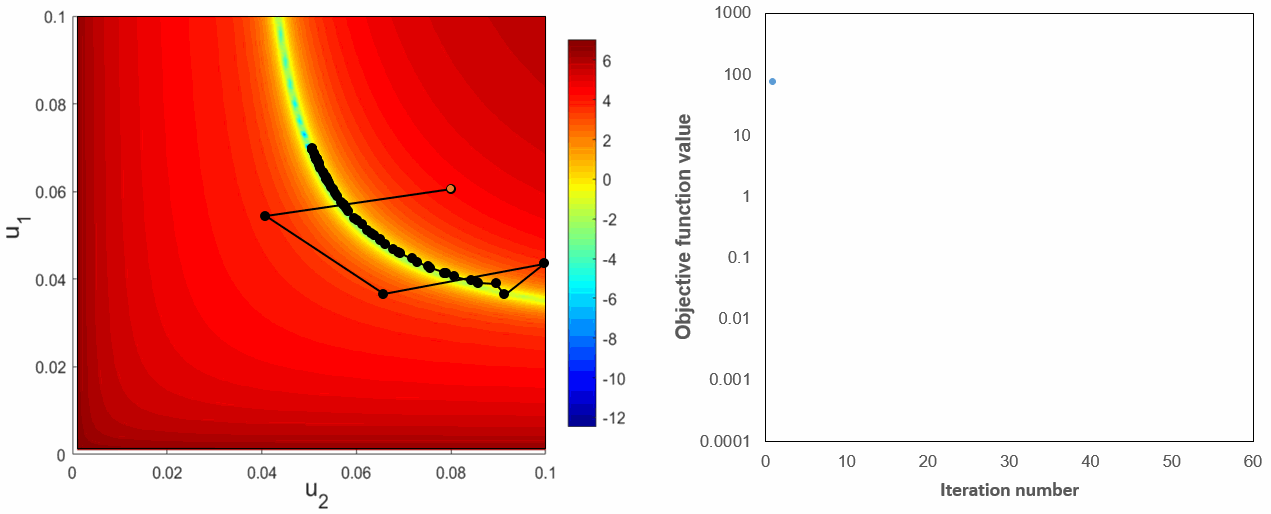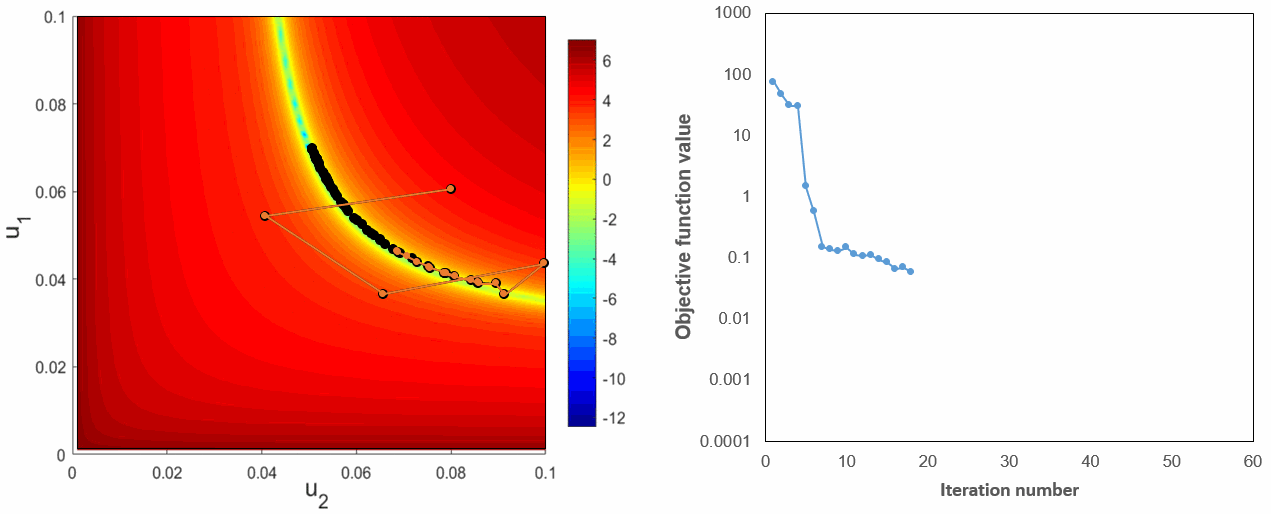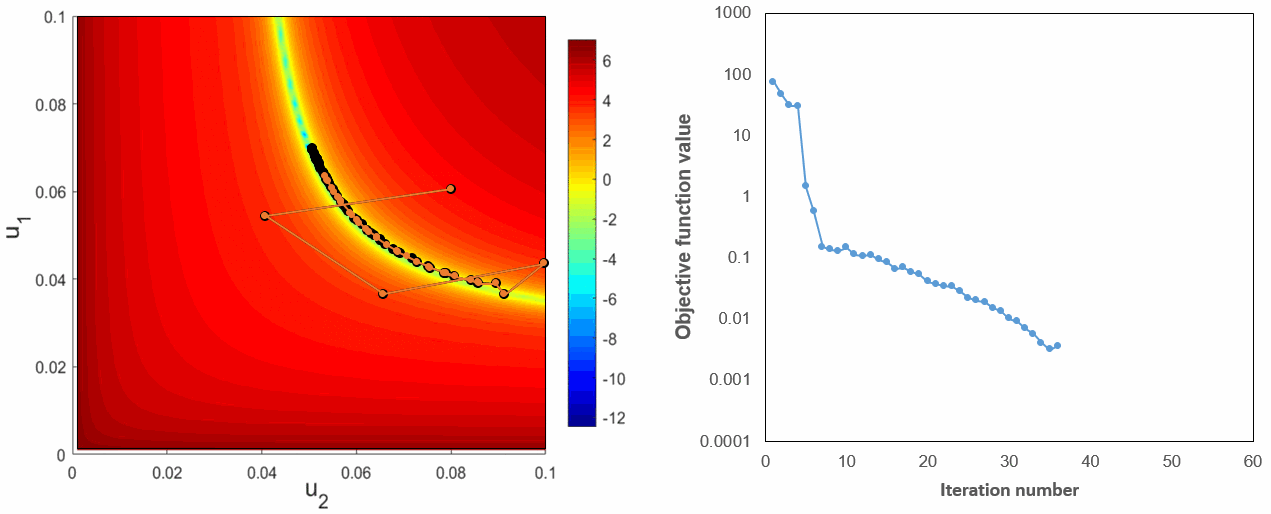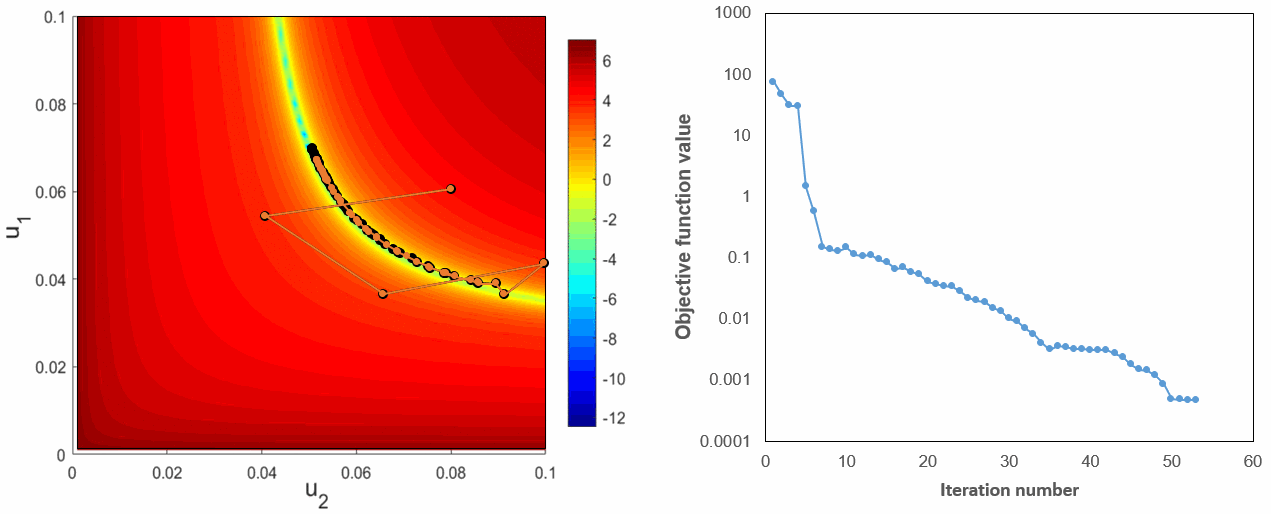
Fig.8: Optimization trajectories with black and orange lines corresponds to numerical and adjoint-based gradients respectively (left) and objective function reduction with iterations (right).
Fully-coupled geomechanics
Seismic activity caused by field development has become a reason for public concern in the Netherlands, Germany and United States that resulted in cut or even stop of energy production projects. The nature of such events is a stick-slip frictional instability of pre-existed fractures and faults. Field development causes the redistribution of stresses over the reservoir and surrounding formations which may trigger seismic rupture at critically stressed discontinuities.
We are developing the approach based on the poromechanical simulation that incorporates contact mechanics for fractures. Finite Volume Method with multi-point discretization is used for both mass and momentum balance equations11 . Such approach allows to obtain solution using collocated grid and subsequently to use effective preconditioning strategies for linear system. Discrete Fracture Model is employed to accurately resolve prescribed fractures in unstructured grid. Fully implicit coupling is used to obtain unconditionally stable solution and to create the basis for the investigation of applicability and performance of sequential coupling techniques for this particular problem. Incorporated nonlinearities resulted from inelastic response of the rock, fault weakening or multiphase multicomponent flow is handled using OBL approach.
The main goal of the project is to use this modelling framework to perform simulation of ongoing experimental investigations of soil compaction and frictional response at core-scale. Model adaptation on experimental results will allow to estimate the contribution of different factors causing fault reactivation and to approach to the upscaling of constitutive laws for field-scale predictive modelling of induced seismicity. An example of mechanical displacement for a simple problem when material is pushed from left boundary at different types of unstructured meshes is shown in Fig.9. Fixed top and bottom boundaries cause high shear stresses near left corners and vertical expansion deeper in the body.

 DARTS - Delft Advanced Research Terra Simulator
DARTS - Delft Advanced Research Terra Simulator